算法刷题周记04

岛屿数量（题号：200）

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

解法（DFS）

class Solution
{
public:
    bool inArea(vector> &grid, int r, int c)
    {
        return 0 <= r && r < grid.size() && 0 <= c && c < grid[0].size();
    }
    void dfs(vector> &grid, int r, int c)
    {
        if (!inArea(grid, r, c))
        {
            return;
        }
        if (grid[r][c] != '1')
        {
            return;
        }
        grid[r][c] = '2';

        dfs(grid, r - 1, c);
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r, c + 1);
    }
    int numIslands(vector> &grid)
    {
        int res = 0;
        for (int r = 0; r < grid.size(); r++)
        {
            for (int c = 0; c < grid[0].size(); c++)
            {
                if (grid[r][c] == '1')
                {
                    dfs(grid,r,c);
                    res++;
                }
            }
        }
        return res;
    }
};

子树中标签相同的节点数（题号:1519）

给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0 到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges 。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的 节点的标签就是 labels[i] ）

边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。

返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。

树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。

示例 1：

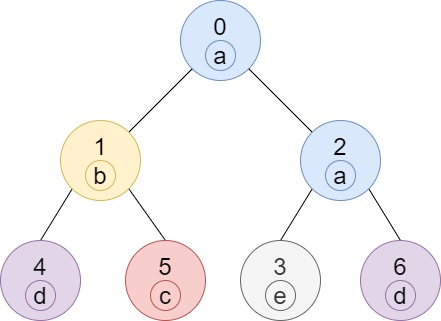
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出：[2,1,1,1,1,1,1]
解释：节点 0 的标签为 'a' ，以 'a' 为根节点的子树中，节点 2 的标签也是 'a' ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。

示例 2：

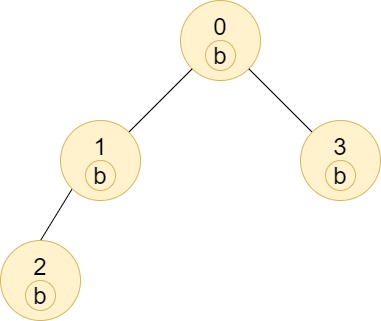
输入：n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出：[4,2,1,1]
解释：节点 2 的子树中只有节点 2 ，所以答案为 1 。
节点 3 的子树中只有节点 3 ，所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ，标签都是 'b' ，因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3，标签都是 'b'，因此答案为 4 。

示例 3：

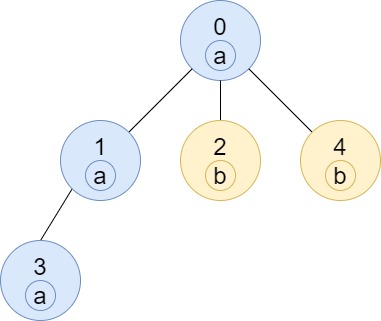
输入：n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出：[3,2,1,1,1]

提示：

• 1 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• labels.length == n
• labels 仅由小写英文字母组成

解法（深度优先遍历）

class Solution {
    String labels;
    private List<Integer>[] adjacentNode;//邻接表,存放每个节点的父节点与所有子节点
    int[][] counts;

    /**
     *
     * @param n 节点数
     * @param edges 所有边
     * @param labels 所有结点对应的标签值
     * @return
     */
    public int[] countSubTrees(int n, int[][] edges, String labels) {
        this.labels = labels;
        adjacentNode = new List[n];
        for (int i = 0; i < n; i++) {
            adjacentNode[i] = new ArrayList<Integer>();
        }
        for (int[] edge : edges) {
            //  父节点      /    子结点
            int node0 = edge[0],node1 = edge[1];
            adjacentNode[node0].add(node1);
            adjacentNode[node1].add(node0);
        }
        counts = new int[n][26];// 记录标签值(26个字母)
        postOrder(0,-1);// 从根节点开始后续遍历
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            char c = labels.charAt(i);
            ans[i] = counts[i][c - 'a'];
        }
        return ans;
    }

    /**
     *
     * @param node 当前节点
     * @param parent 父节点
     */
    public void postOrder(int node,int parent){
        char c = labels.charAt(node);
        List<Integer> adjacent = adjacentNode[node];
        for (Integer next : adjacent) { // 对于每个节点的邻接点
            if (next == parent){
                continue;
            }
            postOrder(next,node);
            // 给每个节点记录标签值 本身+其子节点的标签值
            for (int i = 0; i < 26; i++) {
                counts[node][i] += counts[next][i];//子结点的标签值
            }
        }
        counts[node][c - 'a']++;// 本身结点的值
    }
}

两数之和II - 输入有序数组（题号：167）

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

• 2 <= numbers.length <= 3 * 104
• -1000 <= numbers[i] <= 1000
• numbers 按 非递减顺序 排列
• -1000 <= target <= 1000
• 仅存在一个有效答案

解法(二分)

class Solution {
public:
    vector twoSum(vector& numbers, int target) {
        int len = numbers.size();
        int left = 0,right = len - 1;
        int sum = 0;
        while(left < right)
        {
            sum = numbers[left] + numbers[right];
            if(sum == target){
                break;
            }
            if(sum < target){
                left++;
            }else{
                right--;
            }
        }
        return vector {1+left,1+right};
    }
};

翻转对（题号：493）

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个***重要翻转对***。

你需要返回给定数组中的重要翻转对的数量。

示例1：

输入: [1,3,2,3,1]
输出: 2

示例 2:

输入: [2,4,3,5,1]
输出: 3

解法(归并排序)

class Solution {
    public int reversePairsRecursive(int[] nums, int left, int right){
        if (left == right){
            return 0;
        }else{
            int mid = (left + right) / 2;
            int n1 = reversePairsRecursive(nums,left,mid);
            int n2 = reversePairsRecursive(nums,mid + 1, right);
            int ret = n1 + n2;

            // 统计下标对的数量
            int i = left;
            int j = mid + 1;
            while (i <= mid)
            {
                while (j <= right && (long) nums[i] > 2 * (long)nums[j])
                {
                    j++;
                }
                ret += j - mid - 1;
                i++;
            }
            // 合并两个数组
            int[] sort = new int[right - left + 1];
            int p1 = left,p2 = mid + 1;
            int p = 0;
            while (p1 <= mid || p2 <= right)
            {
                if (p1 > mid)
                {
                    sort[p++] = nums[p2++];
                }else if(p2 > right){
                    sort[p++] = nums[p1++];
                }else {
                    if (nums[p1] < nums[p2]){
                        sort[p++] = nums[p1++];
                    }else{
                        sort[p++] = nums[p2++];
                    }
                }
            }
            for (int k = 0; k < sort.length; k++) {
                nums[left + k] = sort[k];
            }
            return ret;
        }
    }

    int reversePairs(int[] nums){
        if (nums.length == 0)return 0;
        return reversePairsRecursive(nums,0,nums.length - 1);
    }
}