算法刷题周记02

1.引爆最多的炸弹（中等）

今天建军节，来道和炸弹有关的题。

给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。

炸弹用一个下标从 0 开始的二维整数数组 bombs 表示，其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标，ri 表示爆炸范围的 半径 。

你需要选择引爆 一个 炸弹。当这个炸弹被引爆时，所有 在它爆炸范围内的炸弹都会被引爆，这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。

给你数组 bombs ，请你返回在引爆 一个 炸弹的前提下，最多 能引爆的炸弹数目。

示例 1：

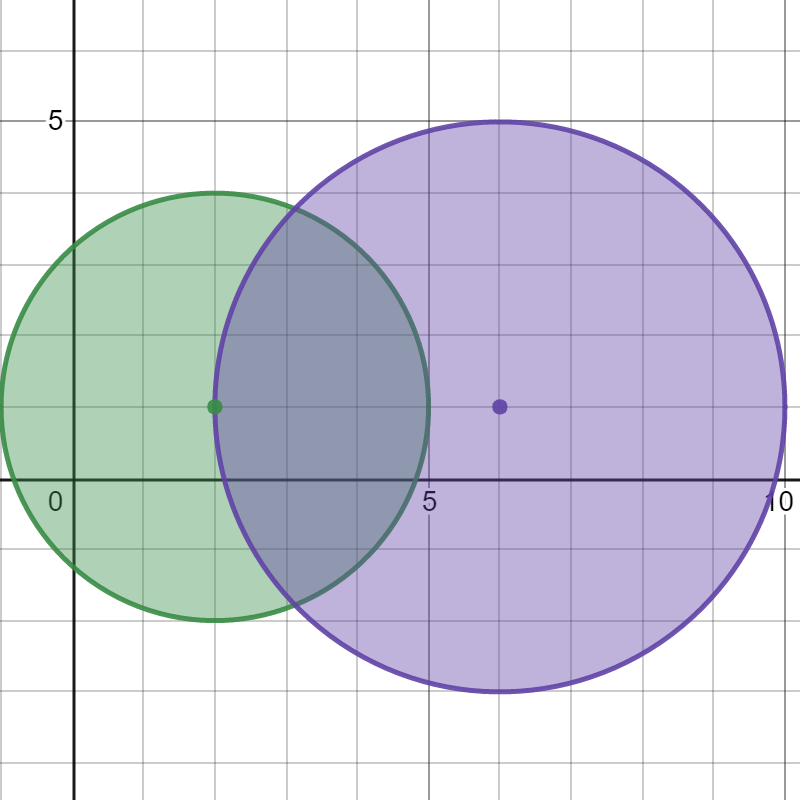
输入：bombs = [[2,1,3],[6,1,4]]
输出：2
解释：
上图展示了 2 个炸弹的位置和爆炸范围。
如果我们引爆左边的炸弹，右边的炸弹不会被影响。
但如果我们引爆右边的炸弹，两个炸弹都会爆炸。
所以最多能引爆的炸弹数目是 max(1, 2) = 2 。

示例 2：

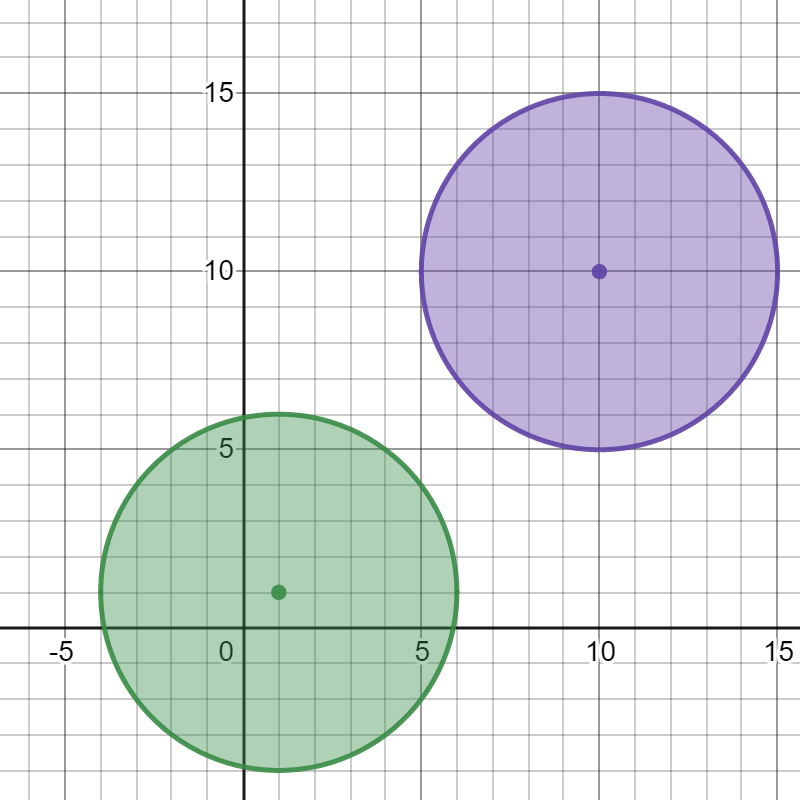
输入：bombs = [[1,1,5],[10,10,5]]
输出：1
解释：
引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。

示例 3：

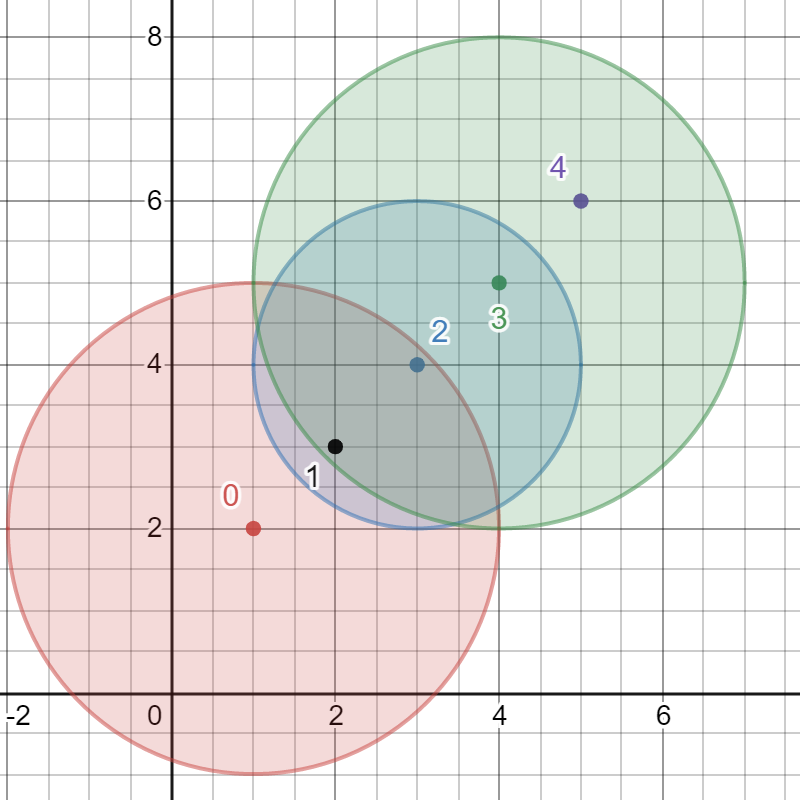
输入：bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
输出：5
解释：
最佳引爆炸弹为炸弹 0 ，因为：
- 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。
- 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。
- 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。
所以总共有 5 个炸弹被引爆。

提示：

• 1 <= bombs.length <= 100
• bombs[i].length == 3
• 1 <= xi, yi, ri <= 105

解法（DFS）

class Solution {
    // 判断通过炸弹i是否可以引爆炸弹j
    public boolean isDetonates(int i,int j,int [][]bombs){
        long dx = (bombs[i][0] - bombs[j][0]);
        long dy = (bombs[i][1] - bombs[j][1]);
        long dd = dx*dx + dy*dy; // 两点距离平方
        return (dd <= (long) bombs[i][2] * bombs[i][2]);
    }
    public int maximumDetonation(int[][] bombs){
        int n = bombs.length;
        Map<Integer,List<Integer>> edges = new HashMap<>();
        for (int i = 0; i < n; i++) {
            List<Integer> edge = new ArrayList<>();
            for (int j = 0; j < n; j++) {
                if (i != j && isDetonates(i,j,bombs)){
                    edge.add(j);
                }
            }
            edges.put(i,edge);
        }
        int result = 0;// 最多引爆数量
        for (int i = 0; i < n; i++) { // 每个炸弹都尝试一遍
            boolean[] visited = new boolean[n];
            int cnt = 1;
            Queue<Integer> queue = new LinkedList<>();
            queue.add(i);
            visited[i] = true;
            while(!queue.isEmpty())
            {
                Integer sid = queue.peek();
                queue.remove(sid);
                for (Integer cid : edges.get(sid)) {
                    if (visited[cid]) { // 炸弹是否已经被引爆
                        continue;
                    }
                    queue.add(cid);
                    visited[cid] = true; // 引爆连接的炸弹
                    cnt++;
                }
            }
            result = Math.max(cnt,result);
        }
        return result;
    }
}

2.最长回文子串（中等）

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

解法（暴力法）

public String longestPalindrome(String s) {
    int len = s.length();
    if (len < 2) {
        return s;
    }
    int maxLen = 1; 
    int begin = 0; //回文起始位置
    char[] chars = s.toCharArray();
    for (int i = 0; i < len - 1; i++) { // 从第一个位置开始检测是不是回文
        for (int j = i + 1; j < len; j++) {
            if (j - i + 1 > maxLen && isValidPalindrome(chars,i,j)){
                maxLen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substring(begin,begin+maxLen);

}
private static boolean isValidPalindrome(char[] chars, int i, int j) {
    while(i < j)
    {
        if (chars[i] != chars[j])
        {
            return false;
        }
        i++;
        j--;
    }
    return true;
}

暴力法的时间复杂度为$O(n^3)$

解法二（动态规划）

状态：dp[i][j]表示子串s[i..j]是否为回文子串

得到状态转移方程：dp[i][j]=(s[i] == s[j]) and dp[i+1][j-1]

边界条件： j - 1 - （i + 1） + 1 < 2，整理得 j - i < 3

初始化: 对角线元素 dp[i][i]全为true

public String longestPalindrome(String s) {
    int len = s.length();
    if (len < 2){
        return s;
    }dp
    boolean[][] dp = new boolean[len][len];// dp数组
    for (int i = 0; i < len; i++) {
        dp[i][i] = true;
    }
    char[] charArray = s.toCharArray();
    int maxLen = 1;// 最大回文串长度
    int begin = 0; // 起始位置
    for (int j = 1; j < len; j++) {
        for (int i = 0; i < j; i++) {
            if (charArray[i] != charArray[j]){
                dp[i][j] = false;
            }else{
                if (j - i < 3){
                    dp[i][j] = true;
                }else {
                    dp[i][j] = dp[i + 1][j - 1];
                }
            }
            if (dp[i][j] && j - i + 1 > maxLen)
            {
                maxLen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substring(begin,begin+maxLen);
}

解法三（中心扩散法）

假设 回文 由 中间部分 + 两边部分组成，中间部分全为重复元素。

public String longestPalindrome(String s) {
    int len = s.length();
    // 边界判断1
    if (len < 2){
        return s;
    }
    int[] range = new int[2];// 起始位置，终止位置 的下标
    char[] chars = s.toCharArray();
    for (int i = 0; i < len; i++) {
        i = expandFindLongest(chars,i,range);
    }
    return s.substring(range[0],range[1] + 1);
}
/**
     * 中心扩散式查找，首先检验中间部位是否为重复元素，然后从中间部分low到high开始左右扩散，然后记录最大长度
     * @param chars
     * @param low
     * @param range
     * @return 中心部位最后一个字符
     */
public int expandFindLongest(char[] chars,int low,int[] range){
    int high = low;
    while (high < chars.length - 1 && chars[high + 1] == chars[low])
    {
        high++;
    }
    int ans = high;// ans 为回文中间部分重复元素的最后一个
    while(low > 0 && high < chars.length - 1 && chars[low - 1] == chars[high + 1])
    {
        low--;
        high++;
    }
    if (high - low > range[1] - range[0])
    {
        range[0] = low;
        range[1] = high;
    }
    return ans;
}

3.搜索旋转排序数组（中等）

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k （0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如，[0,1,2,4,5,6,7]在下标3处经旋转后可能变为[4,5,6,7,0,1,2]。

给你 旋转后 的数组 nums 和一个整数 target ，如果nums中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为O(log n)的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• nums 中的每个值都 独一无二
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -104 <= target <= 104

解法(二分查找)

先介绍一下二分查找。。

二分查找是在一个有序的数组中查找的算法，通过二分查找可以快速的缩小范围；

算法步骤：

1. 申明三个变量，指示待查找区域的起点，中点，末点
2. 将数组的中间项与 Target 进行比较，如果 Target 比数组的中间项要小，则到数组的前半部分继续查找，反之，则到数组的后半部分继续查找。
3. 如果找到则返回，否则重复2的操作，最终就会在数组中找到T，或者确定原以为T所在的范围实际为空。

/**
 * @brief 将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。此时有序部分用二分法查找。
 *        无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.
 * @param nums 
 * @param target 
 * @return int 
 */
int search(vector& nums, int target) {
    int low = 0, high = nums.size() - 1;
    while (low <= high)
    {
        int mid = low + ((high - low)>>2); // 中间元素下标
        if (target == nums[mid])
        {
            return mid;
        }
        // 如果中间的数小于最右边的数，则右半段是有序的
        if(nums[mid] < nums[high])
        {
            if (target > nums[mid] && target <= nums[high]) // 目标值在有序的那一半数组
            {
                low = mid + 1;
            }else{ // 目标值在无序的那一半数组
                high = mid - 1;
            }
        }else{ // 如果中间的数大于最右边的数，则左半段是有序的
            if (target < nums[mid] && target >= nums[low])// 目标值在有序的那一半数组
            {
                high = mid - 1;
            }else{// 目标值在无序的那一半数组
                low = mid + 1;
            }
        }
    }
    return -1;
}

4.LRU 缓存（中等）

一个算法设计题。

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字key已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

解法（Java中的LinkedHashMap）

这个题就是让你理解Java中的LinkedHashMap，具体可以看看这篇文章: 源于LinkedHashMap源码。

代码如下：

public class LRUCache extends LinkedHashMap<Integer,Integer> {
    private int capacity;

    public LRUCache(int capacity) {
        super(capacity,0.75F,true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key,-1);
    }

    public void put(int key, int value) {
        super.put(key,value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    }
    // 自己写的测试
    public static void main(String[] args) {
        LRUCache1 c1 = new LRUCache(2);
        c1.put(1,1);
        c1.put(2,2); // 2=2, 1=1
        System.out.println(c1.get(1)); //输出 1  1=1, 2=2
        c1.put(3,3);// 3=3 , 1=1
        System.out.println(c1.get(2));// 输出 -1
        c1.put(4,4);// 4=4,3=3
        System.out.println(c1.get(1));// 输出-1
        System.out.println(c1.get(3));// 输出 3
        System.out.println(c1.get(4));// 输出 4
    }
}

5.删除链表的倒数第 N 个结点（中等）

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例2：

输入：head = [1], n = 1
输出：[]

示例3：

输入：head = [1,2], n = 1
输出：[1]

解法（双指针）

就是做两个指针，第一个指针先走k步，然后第一第二指针一起走，等第一指针走到尾部时，第二指针正好落后k步。

如此一来，很好理解

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(-1,head);
        ListNode *p,*q;
        p = dummy;
        q = p->next;
        while(n-- && q != NULL ) //使得 p 和 q 之间 有 n 个结点
        {
            q = q->next;
        }
        while(q != NULL)
        {
            p = p->next;
            q = q->next;
        }
        // p 此时到达倒数第n个结点的前一个结点
        ListNode *delNode = p->next;
        p -> next = delNode -> next;
        delete delNode;
        return dummy->next;
    }
};

基本来说，双指针能解决很多问题，比如一前一后同步走，或者一个走一步一个走两步，检测单链表的环。

6.函数的独占时间

有一个 单线程 CPU 正在运行一个含有 n 道函数的程序。每道函数都有一个位于 0和n-1之间的唯一标识符。

函数调用 存储在一个 调用栈 上 ：当一个函数调用开始时，它的标识符将会推入栈中。而当一个函数调用结束时，它的标识符将会从栈中弹出。标识符位于栈顶的函数是 当前正在执行的函数 。每当一个函数开始或者结束时，将会记录一条日志，包括函数标识符、是开始还是结束、以及相应的时间戳。

给你一个由日志组成的列表 logs ，其中logs[i]表示第i条日志消息，该消息是一个按 "{function_id}:{"start" | "end"}:{timestamp}" 进行格式化的字符串。例如，"0:start:3" 意味着标识符为 0 的函数调用在时间戳 3 的 起始开始执行 ；而 "1:end:2" 意味着标识符为 1 的函数调用在时间戳 2 的 末尾结束执行。注意，函数可以 调用多次，可能存在递归调用 。

函数的 独占时间 定义是在这个函数在程序所有函数调用中执行时间的总和，调用其他函数花费的时间不算该函数的独占时间。例如，如果一个函数被调用两次，一次调用执行2单位时间，另一次调用执行 1 单位时间，那么该函数的 独占时间 为 2 + 1 = 3 。

以数组形式返回每个函数的 独占时间 ，其中第 i 个下标对应的值表示标识符 i 的函数的独占时间。

示例 1：

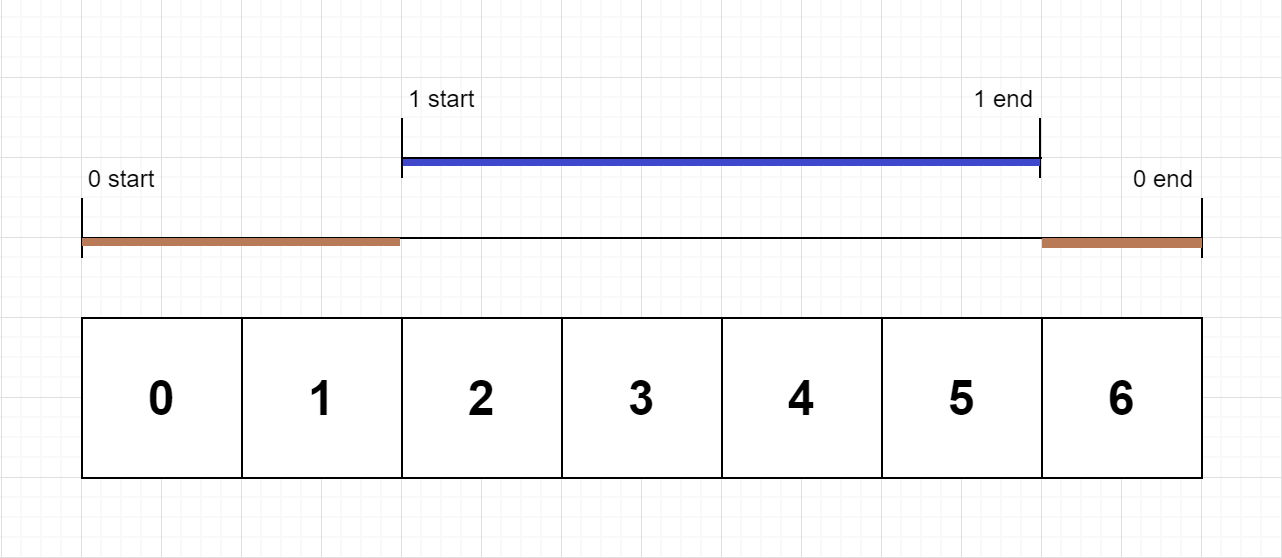
输入：n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"]
输出：[3,4]
解释：
函数 0 在时间戳 0 的起始开始执行，执行 2 个单位时间，于时间戳 1 的末尾结束执行。 
函数 1 在时间戳 2 的起始开始执行，执行 4 个单位时间，于时间戳 5 的末尾结束执行。 
函数 0 在时间戳 6 的开始恢复执行，执行 1 个单位时间。 
所以函数 0 总共执行 2 + 1 = 3 个单位时间，函数 1 总共执行 4 个单位时间。 

示例 2：

输入：n = 1, logs = ["0:start:0","0:start:2","0:end:5","0:start:6","0:end:6","0:end:7"]
输出：[8]
解释：
函数 0 在时间戳 0 的起始开始执行，执行 2 个单位时间，并递归调用它自身。
函数 0（递归调用）在时间戳 2 的起始开始执行，执行 4 个单位时间。
函数 0（初始调用）恢复执行，并立刻再次调用它自身。
函数 0（第二次递归调用）在时间戳 6 的起始开始执行，执行 1 个单位时间。
函数 0（初始调用）在时间戳 7 的起始恢复执行，执行 1 个单位时间。
所以函数 0 总共执行 2 + 4 + 1 + 1 = 8 个单位时间。

示例 3：

输入：n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"]
输出：[7,1]
解释：
函数 0 在时间戳 0 的起始开始执行，执行 2 个单位时间，并递归调用它自身。
函数 0（递归调用）在时间戳 2 的起始开始执行，执行 4 个单位时间。
函数 0（初始调用）恢复执行，并立刻调用函数 1 。
函数 1在时间戳 6 的起始开始执行，执行 1 个单位时间，于时间戳 6 的末尾结束执行。
函数 0（初始调用）在时间戳 7 的起始恢复执行，执行 1 个单位时间，于时间戳 7 的末尾结束执行。
所以函数 0 总共执行 2 + 4 + 1 = 7 个单位时间，函数 1 总共执行 1 个单位时间。 

示例 4：

输入：n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:7","1:end:7","0:end:8"]
输出：[8,1]

示例 5：

输入：n = 1, logs = ["0:start:0","0:end:0"]
输出：[1]

解法（栈）

当函数调用开始时，如果当前有函数正在运行，则当前正在运行函数应当停止，此时计算其的执行时间，然后将调用函数入栈。
当函数调用结束时，将栈顶元素弹出，并计算相应的执行时间，如果此时栈顶有被暂停的函数，则开始运行该函数。
由于每一个函数都有一个对应的 start 和 end 日志，且当遇到一个 end 日志时，栈顶元素一定为其对应的 start 日志。那么我们对于每一个函数记录它的函数标识符和上次开始运行的时间戳，此时我们只需要在每次函数暂停运行的时候来计算执行时间和开始运行的时候更新时间戳即可。

public class Solution {
    public int[] exclusiveTime(int n, List<String> logs) {
        Deque<int[]> stack = new ArrayDeque<>();// 存储每个函数开始的运行时间 [idx,开始运行时间]
        int[] res = new int[n]; // 每个元素的独占时间，下标为函数编号
        for (String log : logs) {
            int idx = Integer.parseInt(log.substring(0, log.indexOf(":")));// 函数编号
            String type = log.substring(log.indexOf(":") + 1, log.lastIndexOf(":"));// 函数调用 开始/退出
            int timestamp = Integer.parseInt(log.substring(log.lastIndexOf(":")+ 1)); // 时间戳
            if ("start".equals(type)) {
                if (!stack.isEmpty()) {
                    res[stack.peek()[0]] += timestamp - stack.peek()[1]; // 计算栈顶函数的一段运行时间，当前时间戳（也就是马上要运行的函数的start时间戳） - 上次push的时间戳
                }
                stack.push(new int[]{idx, timestamp});
            } else {
                int[] t = stack.pop(); // 获取栈顶元素，对应的一定是其start日志
                res[t[0]] += timestamp - t[1] + 1; // 计算运行时间： end的时间戳 - start的时间戳
                if (!stack.isEmpty()) {
                    stack.peek()[1] = timestamp + 1;
                }
            }
        }
        return res;
    }
}